sábado, 17 de febrero de 2018
EJERCICIOS DESARROLLADOS EN CLASE (6B)
Rascacielos de papel
Ejercicio:
En éste ejercicio se realizó un rascacielos que contuviera
los elementos ya descritos en el blog anterior. Se llevó a cabo en equipo con 4
personas.
Los materiales utilizados fueron principalmente hojas de
papel, diurex, y 3 lápices para darle un soporte a la estructura.
El edificio se compone principalmente de dos elementos que
se entrelazan, pero en ese recorrido también deja ver a través de la misma
estructura. La estructura crea mucha dirección y movimiento.
En la parte de abajo está compuesta por pirámides rectangulares
del tamaño de una hoja tamaño carta, la parte siguiente con rollos de la misma
hoja y para dar la forma de la parte más alta usamos las hojas, deformándolas hasta
darle la forma deseada.
Al final se le dio un poco de soporte con unos lápices en la
parte baja. La altura






COMPONER POR ORIENTACIÓN
Componer
| Decode Urbanism Office con sede en Beijing- Movimiento |
El término componer proviene del latín. Deriva del verbo
compono, componis, componere, composui, compositum formado por el prefijo com-
que significa convergencia, reunión y por el verbo pono, ponis, ponere, posui,
positum cuyo significado es poner, colocar, disponer.
En consecuencia el concepto etimológico de este vocablo es poner, disponer
junto a.
Características de composición:
Dirección: Llevar algo hacia un término o lugar, encaminar
las operaciones a un fin, orientar.
Movimiento: Cambio de lugar o de composición de un cuerpo en
el espacio.
 |
| Le corbusier- Dirección |
Quiebre: Romper, doblar o fracturar.
Axial: Relativo al eje.
Contrappossto: designa la oposición armónica de las
distintas partes de la figura humana.
 |
| Quiebre en la arquitectura |
 |
| Simetría axial |
 |
| Contrappossto |
BIBLIOGRAFÍA:
DEFINICIÓN DE COMPOSICIÓN. (2010). Recuperado 17 febrero, 2018, de https://definicion.de/composicion/
EJERCICIOS DESARROLLADOS EN CLASE (4B)
El ejercicio desarrollado en clase fue el siguiente:
Con una tabla de unicel de 2 cm de grosor se trabajo para hacer el borrador del cubo áureo.De la tabla se cortaron 5 cuadros de 10x10 cm, se pegaron uno sobre otro y sobre ésto se trabajo para bocetear nuestro cubo áureo en base a las medidas correspondientes.
 |
| Bocetaje para cubo áureo. |
 |
| Bocetaje para cubo áureo. |
 |
| Bocetaje para cubo áureo. |
 |
| Bocetaje para cubo áureo. |
 |
| Bocetaje para cubo áureo. |
 |
| Bocetaje para cubo áureo. |
PROPORCIÓN ÁUREA (4A)
Proporción Áurea
Leonardo Pisano, también conocido como
Fibonacci, fue un famoso matemático italiano que difundió el gran descubrimiento de Fibonacci fue la Sucesión de Fibonacci
que, posteriormente, dió lugar a la proporción áurea.
El número áureo (1,618034) que se identifica
con la letra Phi del abecedario griego.
La espiral resultante (conocida como Espiral
de Oro o Espiral Aurea) está permanentemente presente en la naturaleza: en las
semillas de un girasol, en las conchas marinas... Componer una imagen siguiendo
esta espiral nos resulta agradable visualmente porque las proporciones que se
obtienen nos parecen naturales.
Rectángulo cuyos lados midan dos de los
números de la serie de Fibonacci

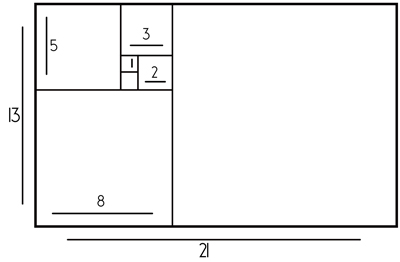
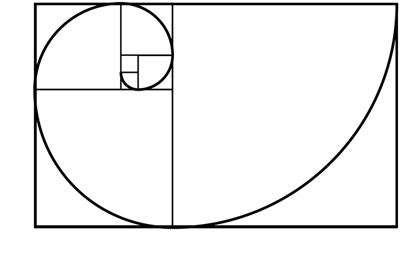
BIBLIOGRAFÍA:
Vidal, M. (2012). Proporción Áurea: Qué Es y Cómo Usarla en la Composición de tus Fotos [Publicación en un blog]. Recuperado 17 febrero, 2018, de https://www.dzoom.org.es/descubre-que-es-la-proporcion-aurea-y-como-puede-ayudarte-en-la-composicion-de-tus-fotos/
TIPOS DE PROPORCIÓN
¨Razones y Proporciones¨
CLASES DE PROPORCIÓN
Proporción
aritmética:
Es la igualdad entre dos razones aritméticas
Ejemplo
Ejemplo
Si 43 excede a 25 como 60 excede a 42, se puede
escribir:
43 – 25 = 60 -42
Dónde:
43 y 60: antecedentes
25 y 42: consecuentes
43 y 42: términos extremo
25 y 60: términos medios
Proporción Geométrica
establece entre dos elementos una razón simple, expresable
como dos múltiplos de una unidad ó módulo: 2/3, 3/5, 1/2 (proporción estática)

La proporción armónica
se basa en las propiedades de la diagonal del cuadrado; es
decir, en las relaciones existentes entre los lados de un cuadrado y su
diagonal. En otras palabras, proporcionar armónicamente implica proporcionar en
base al cuadrado y su diagonal. En un cuadrado de lado igual a 1 a diagonal
vale raíz de 2. Por lo tanto la base de las relaciones armónicas es el número raíz
de 2.
BIBLIOGRAFÍA:
Iturbide, A. (2014). DISEÑO DE INTERIORES Y MOBILIARIO [Publicación en un blog]. Recuperado 17 febrero, 2018, de http://unrn.edu.ar/blogs/disinte-matematica-1/files/2014/03/Unidad-1.pdf
EJERCICIOS DESARROLLADOS EN CLASE
MODULO KEN
Ken: es la unidad tradicional japonesa de la longitud
comparable a la braza inglesa (1.829 metros). El Ken es igual a 6 shaku, que es
cerca de 1.818 metros. El Ken tiene la longitud de un tradicional tatami
acolchado.
Aunque fue utilizado originalmente simplemente para
señalar el intervalo entre dos columnas y variado de tamaño, el ken fue también
un estándar en la arquitectura de residencias. A diferencia del modulo del
Orden Clásico, el cual se basa en el diámetro de una columna y varia con el
tamaño de un edificio, el ken se hizo una medida absoluta.
| Ejemplo ken |
La unidad arquitectónica estandardizada en el Japón era el tatami. Es una cubierta de piso rectangular única que mide 6 shaku y 3 Sun (cerca de 190 cm) de largo por 3 shaku y 1.5 sun (cerca de 95 cm) de ancho, este tipo de tatami fue usado en la región de Kansai.
El tamaño de un cuarto esta determinado por el numero de los pisos acochados tatamis.
En resumen, las unidades de la
longitud son el shaku, el sun, y ken; y su equivalencia entre ellas es:
10 sun son iguales a 1 shaku
 |
| Piso tatami |
6 shaku es igual a un ken
| Piso tatami |
Se desarrollo un ejercicio de un despacho de arquitectura, conteniendo las medidas y características anteriormente mencionadas.
Programa arquitectónico:
-Recepción
-Toilet
-Área de alimentos y descanso
-Área de dibujo
-Baño completo
 |
| Bosquejo |
BIBLIOGRAFÍA:
Ken [Publicación en un blog]. (s.f.). Recuperado 17 febrero, 2018, de http://www.arqhys.com/construccion/ken-medida-modulo.html
PROPORCIÓN
¿Qué es la Proporción?
Proporción es la relación
armoniosa de una parte con otra o con el todo
• “El propósito de
todas las teorías de la proporción es crear un sentido de orden entre los
elementos de una construcción visual.”
• Las proporciones con respecto al tamaño, es la relación de
(medida) entre las partes, y esta relación está determinada por la división
entre un lado y otro, a esta relación se le llama razón.
Clases de proporción
• Geométrica
• Aritmética
• Armónica
•
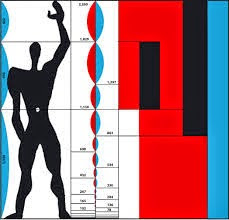 |
| el modulor de le corbusier |
El Modulor sirve para ordenar “las dimensiones de aquello que contiene y de lo que es contenido”
• Considero los
medios de medida de los egipcios y griegos así como de otras culturas ya que
tenían presente las matemáticas y las proporciones del cuerpo humano
Este nuevo sistema debería ser antropométrico, matemático y armónico y por lo tanto basado en la medida de un hombre de 1,83 metros de altura, que con el brazo en alto alcanzaría aproximadamente 2,20 metros.
La Escala
• La escala de un objeto puede cambiar sin cambiar sus
proporciones. Esto quiere decir que su tamaño cambia, puede ser más grande o
más pequeño pero sus relaciones internas se mantienen.
• Cuando la escala se
cambia sin tener en cuenta las proporciones que el objeto tiene, éste se
deforma.
| Escala |
El hombre de Vitruvio
• El Hombre de
Vitruvio es un famoso dibujo acompañado de notas anatómicas de Leonardo da
Vinci realizado alrededor del año 1490 en uno de sus diarios. Representa una
figura masculina desnuda en dos posiciones sobreimpresas de brazos y piernas e
inscrita en una circunferencia y un cuadrado ('Ad quadratum'). Se trata de un
estudio de las proporciones del cuerpo humano, realizado a partir de los textos
de arquitectura de Vitruvio
| El hombre de Vitruvio |
La Secuencia de Fibonacci
Aparece en
configuraciones biológicas, como por ejemplo en las ramas de los árboles, en la
disposición de las hojas en el tallo, en las flores de alcachofas y girasoles,
en las inflorescencias del brécol romanesco y en la configuración de las piñas
de las coníferas.
• La secuencia de Fibonacci es una secuencia infinita de
número que comienza por: 1, 1, 2, 3, 5, 8,13..., en la que cada uno de ellos es
la suma de los dos anteriores.
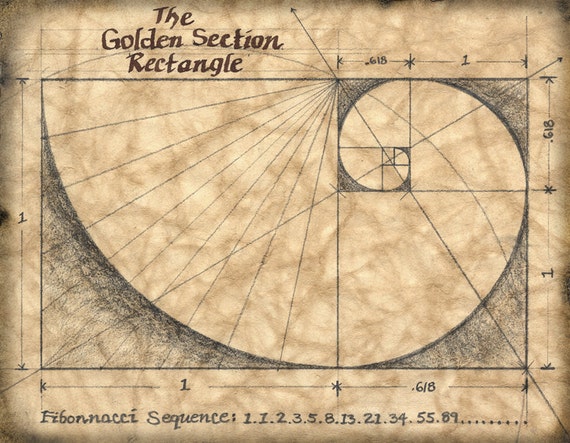 |
| Secuencia Fibonacci |
BIBLIOGRAFÍA:
Contreras, R. (2013, 7 junio). Elementos de relación. Recuperado 5 abril, 2016, de https://es.slideshare.net/RaulContrerasRodriguez/tipos-de-proporcin-60483837
EL FASCINANTE SIGNIFICADO DE "EL HOMBRE DE VITRUVIO" DE LEONARDO DA VINCI [Ilustración]. (2016, 8 julio). Recuperado 17 febrero, 2018, de http://pijamasurf.com/2016/08/el-fascinante-significado-del-hombre-de-vitruvio-de-leonardo-da-vinci/
ESCALA [Publicación en un blog]. (s.f.). Recuperado 17 febrero, 2018, de http://webdelprofesor.ula.ve/nucleotrujillo/alperez/teoria/cap_01c-escala/01-concepto_de_escala.htm
CUBO ÁUREO
DEFINICIÓN DE PROPORCIÓN ÁUREA
La proporción áurea es un número irracional que descubrieron
pensadores de la Antigüedad al advertir el vínculo existente entre dos
segmentos pertenecientes a una misma recta. Dicha proporción puede hallarse en
la naturaleza (flores, hojas, etc.) y en figuras geométricas y se le otorga una
condición estética: aquello cuyas formas respetan la proporción áurea es
considerado bello.
Esta proporción, que también suele mencionarse como razón
áurea, número áureo o divina proporción, incluso solía ser señalada por sus
supuestas propiedades místicas. Su ecuación se expresa como 1 más la raíz
cuadrada de 5, todo sobre 2, y el resultado es aproximadamente igual a
1,61803398874989…

La representación gráfica de la proporción áurea, que se
obtiene trazando una serie de rectángulos y uniendo algunos de sus vértices con
una línea espiralada, da como resultado la conocida Espiral de Oro
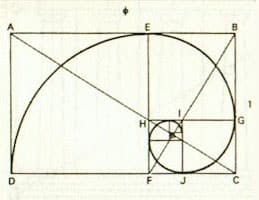
Maqueta cubo áureo:
Esta maqueta fue realizada en base al número áureo, sacando medidas respecto al mismo.
Cubo de 20x20 el cual se encuentra dividido en 3 partes. El planteamiento fue:


Para hacer el bocetaje se utilizo un cubo de unicel de 10x10 en base a las medidas obtenidas como se ve a continuación:
 |
| Boceto. |
 |
| Proceso. |
DOMINANCIA
Maqueta
Ésta maqueta hecha a partir de unicel, representa una de las esculturas del blog pasado.
Se representa más grande y es el adjetivo CREATIVIDAD.

Esta maqueta contiene los elementos dominante, subdominante y subordinado
EJERCICIOS DESARROLLADOS EN CLASE
La relación de entre dos o más elementos. Si dichos elementos se diseñan adecuadamente, se logra una imagen agradable del conjunto con la simple unión de elementos rectilíneos.
Se da jerarquía a los elementos de un diseño como dominante, subdominante y subordinado.
El ejercicio de la semana consistía principalmente en realizar un análisis de nuestras características, dibujando algo sencillo que las representara. Después hacer una pequeña escultura con tan solo tres formas, una escultura que abstrajera el concepto de nuestro dibujo. Donde se pudieran distinguir de las formas cual sería la dominante, subdominante y subordinada.
En la clase de esta semana principalmente aprendimos sobre la diferencia entre relación y proporción.
Se muestran las 10 esculturas abstractas, con el nombre del adjetivo que me representan. En otra foto, los dibujos que representan a las mismas.
 |
| Dibujos que representan esculturas. |










Suscribirse a:
Comentarios (Atom)







